Category: Read

📗 Started reading Dealing with China by Henry M. Paulson, Jr.

📗 Started reading Dealing with China by Henry M. Paulson, Jr.

Former head of Goldman Sachs and U.S. Treasury Secretary Henry M. Paulson , Jr. and the cover of his 2015 book Dealing with China
Former head of Goldman Sachs and U.S. Treasury Secretary Henry M. Paulson , Jr. and the cover of his 2015 book Dealing with China

🔖 Want to read Dealing with China: An Insider Unmasks the New Economic Superpower by Henry M. Paulson, Jr.

🔖 Want to read Dealing with China: An Insider Unmasks the New Economic Superpower by Henry M. Paulson, Jr.

Picked up a copy at Little Free Library #21797 at 8:29 am
ISBN: 978-1-4555-0421-3 First Edition Hardcover

Former head of Goldman Sachs and U.S. Treasury Secretary Henry M. Paulson , Jr. and the cover of his 2015 book Dealing with China
Former head of Goldman Sachs and U.S. Treasury Secretary Henry M. Paulson , Jr. and the cover of his 2015 book Dealing with China

📕 100.0% done with Fletch’s Moxie by Gregory Mcdonald

📕 100.0% done with Fletch’s Moxie by Gregory Mcdonald

Not sure how I feel about a group of potential suspects showing up in the final act this way. The racists in KKK garb here could certainly have been the motivation for the scenes in the film Fletch Lives.

The plot here was very subtly crafted together and done rather well for a novel format. Things seem to have unraveled so quickly at the end–I wish it had been a tad slower so that I could have enjoyed it longer.

📖 60.0% done with Fletch’s Moxie by Gregory Mcdonald

📖 60.0% done with Fletch’s Moxie by Gregory Mcdonald

This feels more like a drawing room mystery or a book version of Clue rather than a traditional shoe-leather detective story. All the suspects seem to be holed up in a house and conversing as Fletch makes a few calls out for details. In this sense, it’s not a nail-biter, but is focusing more on character than some of the others in the series.

📕 100.0% done with Fletch’s Fortune by Gregory Mcdonald

📕 100.0% done with Fletch’s Fortune by Gregory Mcdonald

The second half read incredibly fast. The plot particularly began unfolding in the end almost too quickly. I wish the last act could have lasted a bit longer.

I really enjoyed the Crystal character and the snide banter she continually spouts with Fletch. The wrap up with Freddie was generally unexpected, but delicious in its oddity in the larger canon. There was surprisingly little talk of Fletch’s ex-wives or even of his potentially adding another to the collection.

Some of my favorite jokes were the chapter headings of the schedule of the conference along with even funnily named rooms in which the sessions were taking place.

I’ll hope to write a longer review shortly.

📖 53.0% done with Fletch’s Fortune by Gregory Mcdonald

📖 53.0% done with Fletch’s Fortune by Gregory Mcdonald

Making good progress, hope to finish tomorrow. There are certainly some interesting characters here, though perhaps feeling like too many, particularly since most seem to potentially have committed the murder.

📖 22.0% done with Fletch’s Fortune by Gregory Mcdonald

📖 22.0% done with Fletch’s Fortune by Gregory Mcdonald

Things have slowed down a smidge, but the forward momentum of the murder investigation begins to move things along a bit.

📖 68.0% done with Fletch by Gregory Mcdonald

📖 68.0% done with Fletch by Gregory Mcdonald

This just keeps getting better. I’m enjoying some of the subtle differences between the film and the book. No surprise that the movie renamed Joan Collins to Boyd. I know I’d read this 20+ years ago and I remember it being darker than the film, but the tone seems lighter to me now somehow.

📖 5.0% done with Complex Analysis by Elias M. Stein & Rami Shakarchi

📖 5.0% done with Complex Analysis by Elias M. Stein & Rami Shakarchi

A nice beginning overview of where they’re going and philosophy of the book. Makes the subject sound beautiful and wondrous, though they do use the word ‘miraculous’ which is overstepping a bit in almost any math book whose history is over a century old.

Their opening motivation for why complex instead of just real:

However, everything changes drastically if we make a natural, but misleadingly simple-looking assumption on f: that it is differentiable in the complex sense. This condition is called holomorphicity, and it shapes most of the theory discussed in this book.

We shall start our study with some general characteristic properties of holomorphic functions, which are subsumed by three rather miraculous facts:

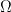
  1. Contour integration: If f is holomorphic in \Omega , then for appropriate closed paths in \Omega

    \int\limits_\gamma f(z)\,\mathrm{d}z = 0.

  2. Regularity: If f is holomorphic, then f is indefinitely differentiable.
  3. Analytic continuation: If f and g are holomorphic functions in \Omega which are equal in an arbitrarily small disc in \Omega , then f = g everywhere in \Omega .

This far into both books, I think I’m enjoying the elegance of Stein/Shakarchi better than Ahlfors.