Arriving from Europe with diamonds in his shoes (hidden there), he found renown in his field with real-world applications, like charting a stock market.
A nice overview of some of Stein’s work.
Arriving from Europe with diamonds in his shoes (hidden there), he found renown in his field with real-world applications, like charting a stock market.
A nice overview of some of Stein’s work.
A nice beginning overview of where they’re going and philosophy of the book. Makes the subject sound beautiful and wondrous, though they do use the word ‘miraculous’ which is overstepping a bit in almost any math book whose history is over a century old.
Their opening motivation for why complex instead of just real:
However, everything changes drastically if we make a natural, but misleadingly simple-looking assumption on
that it is differentiable in the complex sense. This condition is called holomorphicity, and it shapes most of the theory discussed in this book.
We shall start our study with some general characteristic properties of holomorphic functions, which are subsumed by three rather miraculous facts:
- Contour integration: If
is holomorphic in
, then for appropriate closed paths in
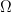
- Regularity: If
is holomorphic, then
is indefinitely differentiable.
- Analytic continuation: If
and
are holomorphic functions in
which are equal in an arbitrarily small disc in
, then
everywhere in
.
This far into both books, I think I’m enjoying the elegance of Stein/Shakarchi better than Ahlfors.