There’s a palm tree in my wine
Discovered a new Little Free Library #11719 at 1000 Stratford Ave. and Mission
🔖 Human Evolution: Our Brains and Behavior by Robin Dunbar (Oxford University Press)
Official release date: November 1, 2016
09/14/16: downloaded a review copy via NetGalley
Description
The story of human evolution has fascinated us like no other: we seem to have an insatiable curiosity about who we are and where we have come from. Yet studying the “stones and bones” skirts around what is perhaps the realest, and most relatable, story of human evolution – the social and cognitive changes that gave rise to modern humans.In Human Evolution: Our Brains and Behavior, Robin Dunbar appeals to the human aspects of every reader, as subjects of mating, friendship, and community are discussed from an evolutionary psychology perspective. With a table of contents ranging from prehistoric times to modern days, Human Evolution focuses on an aspect of evolution that has typically been overshadowed by the archaeological record: the biological, neurological, and genetic changes that occurred with each “transition” in the evolutionary narrative. Dunbar’s interdisciplinary approach – inspired by his background as both an anthropologist and accomplished psychologist – brings the reader into all aspects of the evolutionary process, which he describes as the “jigsaw puzzle” of evolution that he and the reader will help solve. In doing so, the book carefully maps out each stage of the evolutionary process, from anatomical changes such as bipedalism and increase in brain size, to cognitive and behavioral changes, such as the ability to cook, laugh, and use language to form communities through religion and story-telling. Most importantly and interestingly, Dunbar hypothesizes the order in which these evolutionary changes occurred-conclusions that are reached with the “time budget model” theory that Dunbar himself coined. As definitive as the “stones and bones” are for the hard dates of archaeological evidence, this book explores far more complex psychological questions that require a degree of intellectual speculation: What does it really mean to be human (as opposed to being an ape), and how did we come to be that way?
🔖 Complex Analysis by Elias M. Stein & Rami Shakarchi
📖 5.0% done with Complex Analysis by Elias M. Stein & Rami Shakarchi
A nice beginning overview of where they’re going and philosophy of the book. Makes the subject sound beautiful and wondrous, though they do use the word ‘miraculous’ which is overstepping a bit in almost any math book whose history is over a century old.
Their opening motivation for why complex instead of just real:
However, everything changes drastically if we make a natural, but misleadingly simple-looking assumption on
that it is differentiable in the complex sense. This condition is called holomorphicity, and it shapes most of the theory discussed in this book.
We shall start our study with some general characteristic properties of holomorphic functions, which are subsumed by three rather miraculous facts:
- Contour integration: If
is holomorphic in
, then for appropriate closed paths in
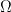
- Regularity: If
is holomorphic, then
is indefinitely differentiable.
- Analytic continuation: If
and
are holomorphic functions in
which are equal in an arbitrarily small disc in
, then
everywhere in
.
This far into both books, I think I’m enjoying the elegance of Stein/Shakarchi better than Ahlfors.
📖 5.0% done with Complex Analysis by Lars V. Ahlfors
🔖 Complex Analysis by Lars Ahlfors
📖 71% done with Carioca Fletch (Fletch #7) by Gregory McDonald
Every gas station should be changed into a pocket park
Introduction to Galois Theory | Coursera
A very beautiful classical theory on field extensions of a certain type (Galois extensions) initiated by Galois in the 19th century. Explains, in particular, why it is not possible to solve an equation of degree 5 or more in the same way as we solve quadratic or cubic equations. You will learn to compute Galois groups and (before that) study the properties of various field extensions. We first shall survey the basic notions and properties of field extensions: algebraic, transcendental, finite field extensions, degree of an extension, algebraic closure, decomposition field of a polynomial. Then we shall do a bit of commutative algebra (finite algebras over a field, base change via tensor product) and apply this to study the notion of separability in some detail. After that we shall discuss Galois extensions and Galois correspondence and give many examples (cyclotomic extensions, finite fields, Kummer extensions, Artin-Schreier extensions, etc.). We shall address the question of solvability of equations by radicals (Abel theorem). We shall also try to explain the relation to representations and to topological coverings. Finally, we shall briefly discuss extensions of rings (integral elemets, norms, traces, etc.) and explain how to use the reduction modulo primes to compute Galois groups.
It’s being offered by National Research University – Higher School of Economics (HSE) in Russia.
[1609.02422] What can logic contribute to information theory?
Logical probability theory was developed as a quantitative measure based on Boole's logic of subsets. But information theory was developed into a mature theory by Claude Shannon with no such connection to logic. But a recent development in logic changes this situation. In category theory, the notion of a subset is dual to the notion of a quotient set or partition, and recently the logic of partitions has been developed in a parallel relationship to the Boolean logic of subsets (subset logic is usually mis-specified as the special case of propositional logic). What then is the quantitative measure based on partition logic in the same sense that logical probability theory is based on subset logic? It is a measure of information that is named "logical entropy" in view of that logical basis. This paper develops the notion of logical entropy and the basic notions of the resulting logical information theory. Then an extensive comparison is made with the corresponding notions based on Shannon entropy.
Based on a cursory look of his website(s), I’m going to have to start following more of this work.
📖 61.0% done with Carioca Fletch (Fletch #7) by Gregory McDonald
The plot seems to have slowed down significantly since the opening, but is just finally getting moving again.
Attending WordCamp Los Angeles

Instagram filter used: Clarendon
Photo taken at: California State University, Los Angeles






